اندازه اثر، آمادگی آزمون دکتری

اندازه اثر، آمادگی آزمون دکتری
نویسنده: دکتر افشین صفایی

 مقدمه 

بیشتراز یک قرن ازبوجود آمدن اکثر آزمون‌های فرض و تحلیل‌های آماری مانند تی استیودنت،ضریب همبستگی پیرسون و … و بدنبال آن‌ها،آزمون‌های معنی داری آماری می‌گذرد. اما دراین مدت همواره انتقاداتی بر آزمون‌های معناداری وارد بوده است. این انتقادات گاهی بشدت سنگین بوده وگاهی مانند اشمیت و هانتر(۱۹۹۷) معتقدند، آزمون‌های معنی داری رشد علمی رابه تعویق انداخته وکمکی به رشدعلمی نمی‌کند. حتی اگراین نوع از انتقادات تندرا نابجابدانیم، سؤال اینجا خواهدبود که درکناراین روش‌ها ویابه‌جای آن‌ها ازچه تکنیک‌هایی می‌توان استفاده‌کرد.

اندازه اثر (Effect Size)

دردهه ۹۰ میلادی مقالاتی منتشرشدکه درآن‌ها دونوع شواهد معنی‌داری کاربردی مطرح گردیدکه عبارت بودنداز: اندازه اثر و فاصله اطمینان. دراین مقالات آورده‌شده‌است که گزارش و تحلیل اندازه اثر همراه‌با آماره‌های مناسب برای معنی داری،برای تحلیل نتایج یک پژوهش خوب ضروری است. اندازه اثر روشی ساده برای اندازه‌گیری تفاوت بین دو گروه است که دارای مزایای زیادی نسبت به استفاده از آزمون‌های معنی داری آماری به تنهایی است.

اندازه اثر

اندازه اثر بدون درنظرگرفتن اندازه نمونه، بر اندازه تفاوت تاکید می‌کند.
گاهی به دلیل در دسترس نبودن نمونه‌های بزرگ یا سختی در فرآیند نمونه‌گیری یا مواردی ازاین قبیل،معناداری آماری برای قبول یک فرضیه آماری حاصل نمی‌شود.
با این حال، پژوهشگر شهوداً حدس می‌زند که اختلاف معناداری وجود داشته که آزمون آماری به تنهایی نتوانسته آن را نشان دهد.
وجود چنین مواردی در علوم رفتاری، باعث شده تا شاخص‌هایی تنها برای اندازه‌گیری اندازه اثر معرفی شوند(بکر، ۲۰۰۰).

اندازه اثر، آمادگی آزمون دکتری

درخلال سال ۱۹۹۲، بیل کلینتون و جورج بوش برای رسیدن به ریاست جمهوری ایالات متحده مبارزه می‌کردند.
کلینتون به سختی در جایگاه خود در نظرسنجی‌ها قرار داشت. بوش پیشتر به عنوان یک رهبر باتجربه جهان شناخته شده‌بود.
جیمز کارویل،یکی از مشاوران ارشد کلینتون، تصمیم گرفت که برای رسیدن به ریاست جمهوری به تمرکز روی آورد.
باتوجه به تحقیقاتی که وی انجام داد،متوجه شد که باید تمرکز ساده‌ای برای مبارزات انتخاباتی انتخاب کند.
برای این منظور روی تخته وایت بردی نوشت: “این اقتصاد،احمقانه است” و هربارکه بیل کلینتون برای سخنرانی می‌رفت آن‌را درمعرض دیداو قرارمی‌داد.

۱) چرا به اندازه اثر نیاز داریم؟

با یک مثال این سؤال را تبیین می کنیم.
در سال ۲۰۰۲،محققی بنام داوسون(Dowson) برای بررسی تأثیرات ساعات مختلف روز برمیزان یادگیری این سؤال تحقیق رامطرح کرد که آیا کودکان درساعات صبح یادگیری بهتری دارند یادرساعات بعدازظهر؟.
وی برای انجام این پژوهش گروهی متشکل از ۳۸ کودک را بطور تصادفی انتخاب و در آزمایش قرار داد. نیمی از آن‌ها به طورتصادفی برای گوش دادن به یک داستان و پاسخ به سؤالات درمورد آن(بر روی نوار) ​​در۹:۰۰ صبح و نیمه دیگر برای شنیدن دقیق همان داستان و پاسخ به سؤالات مشابه در۳:۰۰ بعدازظهر اختصاص داده شدند.
میزان یادگیری و درک کودکان سپس، ازطریق تعدادسؤالاتی که بدرستی پاسخ داده‌بودند از ۲۰ اندازه‌گیری شد. نمره متوسط ​​ ۱۵٫۲ برای گروه صبح و ۱۷٫۹ برای گروه بعدازظهر باتفاوتی معادل ۲٫۷ محاسبه گردید.

آیا این مقدار تفاوتی که بین نمره صبح و عصر وجود دارد، آنقدر بزرگ هست که نتیجه‌گیری کنیم یادگیری در بعدازظهر از صبح بیشتر است؟
به عبارت دیگر، این میزان تفاوت باید دقیقاً ازچه مقداری بزرگتر باشد تا بتوانیم با قاطعیت اظهارنظر کنیم؟
یکی از راه‌های فائق آمدن براین مشکل این است که مقدار تغییرات نمره‌ها را به صورت متفاوتی درنظر بگیرید.
اگر هیچ‌گونه همپوشانی بین دو گروه وجودنداشته‌باشد وهرفرد درگروه بعدازظهر بهتراز هرفرد درگروه صبح باشد،می‌توان دقیقاً نتیجه گرفت که دوگروه کاملاً باهم متفاوت هستند.
ازسوی دیگر،اگر توزیع نمرات زیاد و بزرگ و میزان همپوشانی نمرات دوگروه بسیاربزرگتراز تفاوت بین آن‌ها باشد،مقدار اثرساعت مطالعه درطول روز روی یادگیری ممکن است کمترمعنی‌دار باشد.

از آنجا که مایک مقدار از تغییرات موجود دریک گروه را درک می‌کنیم،می‌توانیم ازاین به عنوان یک معیار برای مقایسه تفاوت استفاده کنیم.
این ایده در محاسبه اندازه اثر مورد استفاده قرار می‌گیرد.
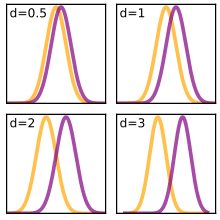
این مفهوم در شکل ۱ نشان داده شده است،که نشان می‌دهد دو روش ممکن است همپوشانی متفاوتی داشته باشند.
اگر تفاوت همانند نمودار(الف) باشد،تفاوت بین دوگروه بسیار قابل‌توجه خواهدبود.
در نمودار (b)، از سوی دیگر، تفاوت ممکن است به سختی قابل توجه باشد.

۲) اندازه اثر چگونه محاسبه می گردد؟

اندازه اثر که معمولاً با d نمایش داده می‌شود، چیزی جز استانداردسازی تفاوت مشاهده‌شده بین دو گروه نیست.
به عبارت دیگر، اندازه اثر از رابطه زیر محاسبه می‌گردد:
این شاخص برای اولین بار توسط کوهن معرفی شده و جز مشهورترین شاخصهای اندازه اثر به شمار می آید.
اگر مشخص نباشد که کدام یک از دو گروه آزمایشی است (به عنوان مثال یک درمان جدید که مورد آزمایش قرار می گیرد) و کدام “کنترل” (که “درمان استاندارد” یا بدون درمان است – برای مقایسه)، همچنان تفاوت قابل محاسبه است.

محاسبه اندازه اثر

در این مورد، ‘اندازه اثر’ به سادگی تفاوت بین آن‌ها را اندازه‌گیری می‌کند،بنابراین هرچه اندازه اثر بزرگتر باشد،تفاوت بین گروه‌ها بیشترخواهدبود.
انحراف استاندارد یک اندازه از توزیع مجموعه‌ای از نمرات است.
در اینجا به انحراف معیار جمعیتی که از گروه های مختلف درمان گرفته شده اشاره می‌شود.
در عمل انحراف معیار تقریبا هرگز شناخته شده نیست، بنابراین باید از انحراف استاندارد گروه کنترل یا از ارزش “مشترک” از هر دو گروه برآورد شود.
در آزمایش اثرات روزانه داوسون در مثال مطرح شده، انحراف معیار SD=3.3 و بنابراین اندازه اثر  برابر ۳٫۳/ (۱۷٫۹ – ۱۵٫۲) = ۰٫۸ خواهد بود.

۳) اندازه اثر چگونه تفسیر می‌گردد؟

در بحث توان آزمون در آزمون‌های فرض نقش اندازه اثر را بر توان آزمون بررسی کردیم.
کاربرد دیگر آماره اندازه اثر، کمک به تفسیر نتایج یک نحقیق منفرد است.
اندازه اثر بزرگتر نشان دهنده تفاوت بیشتر بین دو گروه است.
یکی از ویژگی های اندازه اثر این است که می توان آن را به طور مستقیم به نظراتی در مورد همپوشانی بین دو نمونه با مقایسه صدکها تبدیل کرد.
اندازه اثر دقیقا معادل نمره استاندارد (Z-Score) در یک توزیع نرمال است.

اندازه اثر، آمادگی آزمون دکتری

به عنوان مثال، اگر اندازه اثر برابر با ۰٫۸ باشد، بدان معنی است که نمره میانگین افراد در گروه آزمایش ۰٫۸ انحراف استاندارد بالاتر از میانگین افراد در گروه کنترل است و از این رو نمرات گروه آزمایش از  ۷۹٪ نمرات گروه شاهد بیشتر است.
در دو گروه ۱۹ نفری که برای بررسی وضعیت یادگیری در ساعات صبح و عصر در نظر گرفته شدند، فردی که در گروه بعدازظهر در رتبه دهم قرار دارد، نمره ای تقریبا معادل فردی دارد که در گروه صبح دارای رتبه چهارم است.

اندازه اثر، آمادگی آزمون دکتری

جدول ۱، تبدیل مقادیر اثر (ستون ۱) را به درصد (ستون ۲) و تغییر معادل در رتبه بندی برای یک گروه از ۲۵ نفری (ستون ۳) نشان می‌دهد.
به عنوان مثال، برای اندازه اثر ۰٫۶، مقدار ۷۳٪ نشان می دهد که میانگین فرد در گروه آزمایشی بالاتر از ۷۳٪ از نمره افراد موجود در گروه کنترل است.
احتمال اینکه فردی به تصادف از گروه آزمایش  انتخاب شود و رتبه اش از فرد دیگر در گروه کنترل که او هم به تصادف انتخاب شده است بالاتر باشد.

 

اندازه اثر

درصدی از گروه کنترل که زیر میانگین در گروه آزمایشی

برابری رتبه فرد در دو گروه کنترل و آزمایش ۲۵ نفری

احتمال اینکه از روی نمره فرد بتوان حدس زد آن فرد به کدام گروه تعلق دارد.

همبستگی یکسان  r (اختلاف در درصد موفقیت در افراد هر دو گروه)

۰٫۰

۵۰%

۱۳th

۰٫۵۰

۰٫۰۰

۰٫۵۰

۰٫۱

۵۴%

۱۲th

۰٫۵۲

۰٫۰۵

۰٫۵۳

۰٫۲

۵۸%

۱۱th

۰٫۵۴

۰٫۱۰

۰٫۵۶

۰٫۳

۶۲%

۱۰th

۰٫۵۶

۰٫۱۵

۰٫۵۸

۰٫۴

۶۶%

۹th

۰٫۵۸

۰٫۲۰

۰٫۶۱

۰٫۵

۶۹%

۸th

۰٫۶۰

۰٫۲۴

۰٫۶۴

۰٫۶

۷۳%

۷th

۰٫۶۲

۰٫۲۹

۰٫۶۶

۰٫۷

۷۶%

۶th

۰٫۶۴

۰٫۳۳

۰٫۶۹

۰٫۸

۷۹%

۶th

۰٫۶۶

۰٫۳۷

۰٫۷۱

۰٫۹

۸۲%

۵th

۰٫۶۷

۰٫۴۱

۰٫۷۴

۱٫۰

۸۴%

۴th

۰٫۶۹

۰٫۴۵

۰٫۷۶

۱٫۲

۸۸%

۳rd

۰٫۷۳

۰٫۵۱

۰٫۸۰

۱٫۴

۹۲%

۲nd

۰٫۷۶

۰٫۵۷

۰٫۸۴

۱٫۶

۹۵%

۱st

۰٫۷۹

۰٫۶۲

۰٫۸۷

۱٫۸

۹۶%

۱st

۰٫۸۲

۰٫۶۷

۰٫۹۰

 

اندازه اثر، آمادگی آزمون دکتری

راه دیگری که برای مفهوم سازی همپوشانی از لحاظ احتمال وجود دارد این است که بتوانیم از طریق نمره یک فرد حدس بزنیم که وی متعلق به کدام یک از دو گروه است. اگر اندازه اثر برابربا صفرباشد(یعنی دوگروه یکسان بودند)،آنگاه احتمال درست حدس زدن دقیقاً برابربا نصف یا۰٫۵۰ است.
اگرتفاوت بین دوگروه اندازه اثری برابربا ۰٫۳ ایجادکند،این عددنیز نشان‌دهنده همپوشانی بالا بین دوگروه است و احتمال شناسایی درست گروه‌ها تنها کمی وتا ۰٫۵۶افزایش می‌یابد.
درمورد اندازه اثری برابر با ۱، احتمال درست حدس زدن به ۰٫۶۹ افزایش می یابد.این احتمالات در ستون چهارم جدول (۱) نشان داده شده است.
واضح است که حتی وقتی مقدار اندازه اثر زیاد باشد، همپوشانی بین گروههای آزمایش و کنترل قابل توجه است (و بنابراین احتمال آن هنوز نزدیک به ۰٫۵ است).

اندازه اثر، آمادگی آزمون دکتری

یک روش که بصورت کمی متفاوت برای تفسیر اندازه اثر استفاده می شود، از همبستگی بین میانگین تفاوت استاندارد شده (d) و ضریب همبستگی، r استفاده می‌کند. اگر عضویت گروه را با یک متغیر ساختگی (به عنوان مثال، گروه کنترل را با ۰ و گروه تجربی را با ۱) کدگذاری کنیم و همبستگی بین این متغیر ساختگی و نتیجه اندازه گیری شده محاسبه شود، مقدار r می‌تواند محاسبه گردد.
با درنظرگرفتن برخی مفروضات اضافی، می‌توان به راحتی d را به r با استفاده از معادله تبدیل کرد(کوهن، ۱۹۶۹).

اندازه اثر، آمادگی آزمون دکتری

روزنتال و روبین(۱۹۸۲) با استفاده از یک ویژگی جالب r تفسیر بیشتری را پیشنهاد کردند که عبارت بود از نمایش دوجمله‌ای اندازه اثر[۱] (BESD).
اگر اندازه‌گیری نتیجه منجر به یک دوگانگی ساده شود (به عنوان مثال، این سؤال که،آیا نمره بالاتریا پایین‌تر ازیک مقدارخاص مانند متوسط می‌تواندبه عنوان “موفقیت” یا “شکست” درنظرگرفته شود)، r می‌تواند به عنوان تفاوت در نسبت‌ها در هر دسته معرفی شود.
به عنوان مثال، اندازه اثری معادل ۰٫۲ نشان دهنده تفاوت ۰٫۱  بین نسبت هاست، همانطور که ۴۵٪ از گروه شاهد و ۵۵٪ از گروه درمان تا حدودی به آستانه ‘موفقیت’ رسیده‌اند. با این حال،توجه داشته باشید که اگر نسبت کلی «موفقیت» نزدیک به ۵۰٪ نباشد،این تفسیر می‌تواند تاحدودی گمراه‎کننده باشد.
مقادیر BESD در ستون ۵ از جدول (۱) نشان داده شده است.

اندازه اثر، آمادگی آزمون دکتری

درنهایت،مک گراو و وانگ(۱۹۹۲) آماره “اثر عام زبان مشترک (CLES)” راپیشنهاد کردندکه به‌نظر آن‌هابه‌راحتی توسط غیرمتخصصان آماری قابل‌فهم است که درستون ۶ جدول(۱) نشان داده‌شده‌است.
این آماره مقدار این احتمال را نشان می‌دهد که نمره‌ای که به طورتصادفی ازیک توزیع انتخاب می‌شود(از گروه اول) بیشتراز مقداری باشد که به طورتصادفی از توزیع دیگری (گروه دوم) انتخاب شده باشد. آن‌ها مثالی برای این مطلب ارائه کردند. فرض کنید قد مردان و زنان جوان بالغ را اندازه گرفته‌ایم و میزان اندازه اثر تقریباً برابربا ۲ بدست آمده است،آن‌ها این اندازه اثر را ۰٫۹۲  CLES ترجمه می‌کنند. به عبارت دیگر، در ۹۲ مورد از ۱۰۰، مردان قد بلندتری نسبت به زن‌ها دارند.
لازم به ذکر است که مقادیر در جدول ۱ به فرض توزیع نرمال بستگی دارند.
تفسیر اندازه اثر از لحاظ درصد، بسیار حساس به نقض این فرض است (سوال ۶ در زیر مطالعه کنید).

اندازه اثر، آمادگی آزمون دکتری

روش دیگر برای تفسیر اندازه اثر آن است که آن را با اندازه اثر تفاوت که مشابه است مقایسه کنید.
به عنوان مثال، کوهن(۱۹۶۹) اثر اندازه ۰٫۲ را کوچک توصیف می‌کند و برای آن مثالی مطرح می‌کند.
وی نشان می‌دهدکه برای مثال تفاوت قد دختران ۱۵ساله و۱۶ساله در ایالات متحده دارای این اندازه اثر هستند.
اندازه اثری برابربا۰٫۵را”متوسط” توصیف می‌کند وآن‌رابه اندازه کافی بزرگ می‌داندکه درآن اختلاف برای چشم غیرمسلح قابل‌مشاهده است.
اندازه اثر ۰٫۵ مربوط به تفاوت بین ارتفاع دختران ۱۴ ساله و ۱۸ ساله است.
کوهن اندازه اثر۰٫۸ رابه عنوان “به شدت شناخته‌شده ودرنتیجه بزرگ”توصیف می‌کندوآن رابه تفاوت بین ارتفاع دختران ۱۳ساله و۱۸ساله معادل می‌کند.
به عنوان یک مثال دیگر،او بیان می‌کندکه تفاوت IQ بین دارندگان درجه Ph.D.و”تازه واردان معمولی کالج “بااندازه اثر ۰٫۸قابل‌مقایسه هستند.

۴) چه رابطه‌ای بین اندازه اثر و معنی داری وجود دارد؟

اندازه اثر اندازه اختلاف بین دوگروه راکمی می‌کند وبنابراین ممکن‌است گفته‌شودکه اندازه اثر،اندازه واقعی معنی‌داربودن اختلاف رانشان می‌دهد.
اگر،برای مثال،نتایج داسون درمورداثرات زمان روی یادگیری ممکن‌است بطورعمومی بکاربرده‌شود وممکن است این سؤال پرسیده شودکه”چه مقدار میزان یادگیری دربعدازظهر نسبت به صبح بیشترخواهدبود؟”.
بهترین پاسخی که به این سؤال داده می‌شود، همان اندازه اثر است.
بااین‌حال،درآمارکلمه معنی‎داری غالباًبه معنی‌داری آمار اطلاق می‌گرددکه عبارت‌است ازدرست‌نمایی اختلاف بین دوگروه که ممکن‌است ناشی ازنمونه‌برداری تصادفی باشد.
اگر از یک جامعه دو نمونه برداریم همیشه بین آن‌ها اختلاف وجود خواهد داشت.

اندازه اثر، آمادگی آزمون دکتری

معنی‌داری آماری معمولاً بصورت p-value محاسبه می‌گردد.
این مقداربرابراست با حداقل احتمال آنکه اختلاف درحجم برابر بهصورت تصادفی بروز کند،حتی اگراختلاف واقعی بین دو جامعه وجودنداشته‌باشد.
برای اختلافات بین میانگین‌های دو گروه، p-value بطور طبیعی از طریق آزمون t محاسبه می‌گردد.
برای مثال،اگر(یعنی زیر ۵%)،اختلاف به اندازه کافی بزرگ باشد”معنی‌دار” و درغیراینصورت “غیر معنی‌دار” خوانده می‌شود.
مشکلاتی در استفاده از آزمون‌های معنی‌داری وجود داردکه مهم‌ترین آن‌هااینستکه p-value بخصوص به دو چیزبستگی دارد:اندازه اثر و اندازه نمونه.
اگر اثر خیلی بزرگ باشد،حتی اگر حجم نمونه کوچک باشد،تفاوت معنی‌دار خواهدبود.
اگر حجم نمونه خیلی بزرگ باشد،حتی اگر اندازه اثر کوچک باشد،باز هم تفاوت معنی‌دار است.

رابطه بین اندازه اثر و معنی‌ داری آماری

بطورکلی باید گفت که سطح معناداری آماری و اندازه اثر،اطلاعات جداگانه‌ای به پژوهشگر می‌دهند.
گزارش تنها یکی از آن‌ها می‌تواند منبعی برای خطا باشد.
از طریق اندازه اثر متوجه می‌شویم که متغیرمستقل تا چه اندازه بر متغیروابسته اثر گذاشته است.
اندازه اثر بزرگتر نشان‌دهنده تفاوت بیشتر بین دو گروه است.

۵) حاشیه خطا در اندازه اثر چیست؟

واضح است که اگراندازه اثربرای یک نمونه باحجم بزرگ محاسبه‌شود به‌احتمال زیادمقدارش خیلی صحیح‌ترازوقتی است که حجم نمونه کوچک باشد.
این “حاشیه برای خطا”با استفاده از بحث بازه اطمینان می‌تواند عددی شود وهمان اطلاعاتی را می‌دهدکه درآزمون‌های معنی‌داری استفاده می‌شود.
با استفاده از یک بازه اطمینان ۹۵ درصدی،سطح معنی‌داری ۵ درصدی را انتخاب کرده‌ایم.
برای محاسبه یک سطح اطمینان ۹۵درصدی،فرض براین خواهدبودکه عددی که بدست می‌آوریم یک مقدارصحیح خواهدبود(دراین حالت اندازه اثر۰٫۸ خواهدبود).

حاشیه خطا در اندازه اثر

اما، محاسبه مقدار پراکندگی در این تخمین مستلزم آنستکه از جامعه مکرراً نمونه برداری شود.
برای هر۱۰۰عدد نمونه جدیدی که ازجامعه گرفته می‌شود،براساس تعریف، ۹۵تا از نمونه‌ها اندازه اثری درفاصله اطمینان ۹۵درصدی خواهندداشت.
اگر این بازه اطمینان صفر را شامل شود،می‌توان نتیجه گرفت نتایج از نظر آماری معنی‌دار نیستند.
ازآنجاکه فاصله اطمینان بر اندازه اثر تاکید دارد،استفاده ازآن راه بهتری نسبت به p-value برای تفسیر داده‌هاست.
یکی از فرمول‌هایی که برای محاسبه فاصله اطمینان برای اندازه اثر ارائه شده بوسیله هدج و اولکین(۱۹۸۵) مطرح شده است.

اندازه اثر، آمادگی آزمون دکتری

اگر اندازه اثر تخمین زده شده برابر d باشد و بصورت نرمال توزیع شده‌باشد،خواهیم داشت:
= تعداد افراد در گروه کنترل یا شاهد
= تعداد افراد در گروه آزمایش
بنابراین، یک بازه ۹۵ درصدی برای d برابر است با:
 

۶) چه عواملی بر اندازه اثر مؤثر هستند؟

اگر چه اندازه اثر بسادگی اندازه‌گیری وبراحتی به عنوان اثربخشی متغیر وابسته تفسیر می‌شود،بااین‌حال می‌تواندبه تعدادی از تأثیرات حساس باشند.
بنابراین در استفاده از اندازه اثر بایدتوجه بیشتری شود. برخی از این مسائل در اینجا شرح داده می‌شود:
کدام انحراف معیار؟
اولین مسئله اینست که از کدام انحراف معیار باید استفاده کنیم.
بطور ایده آل،گروه کنترل یا شاهد، بهترین مقدار را برای انحراف معیار ارائه می‌دهد.

[۱] Binominal Effect Size Display

خرید و دانلود محصولات کمک آموزشی کنکور دکتری:

آمار 
روش تحقیق