
پیشفرضهای تحلیل واریانس
اردیبهشت 12, 1398
تحلیل واریانس (ANOVA)- قسمت دوم
اردیبهشت 26, 1398تحلیل واریانس (ANOVA)- قسمت اول
در این صفحه به آموزش مطالبی در مورد تحلیل واریانس (ANOVA) و موارد استفاده از آن پرداخته میشود.
نقشهای که برای آموزش کامل مبحث تحلیل واریانس در نظرگرفته شدهاست در نمودار زیر آورده شدهاست.
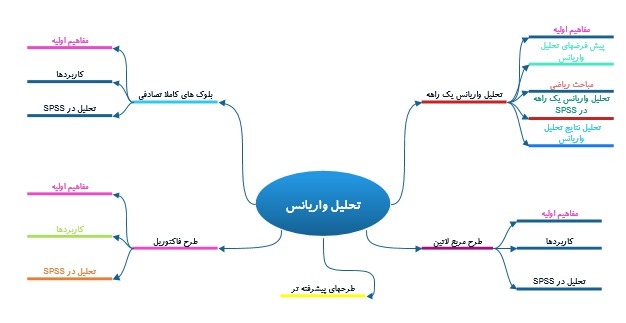
تحلیل واریانس یا همان آنالیز واریانس (Analysis of Variance) مجموعهای از مدلهای آماری و روشهای برآورد همراه با آن است که برای تحلیل اختلافات میان میانگین گروهها در یک نمونه مورداستفاده قرار میگیرد.
ANalysis Of VAriance
ANOVA
قبل از اینکه به تاریخچه و فرضیههای آماری در تحلیل واریانس و پیشفرضهای تحلیل واریانس بپردازیم، با چند مثال پژوهشی موارد استفاده از تحلیل واریانس را با هم بررسی میکنیم.
مثال ۱٫
فرض کنید محققی میخواهد اثر نوشیدن چای در کاهش وزن افراد را بررسی کند.
احتمالاً این پژوهشگر افرادی را به عنوان نمونه از جامعه بصورت تصادفی انتخاب میکند.
متغیر مستقل در این پژوهش میتواند نوع چای مصرفی باشد.
فرض کنید چای معمولی،چای سبز و عدم مصرف چای به عنوان سه سطح از متغیر مستقل درنظرگرفتهشدهاست.
افرادی که به تصادف از جامعه انتخاب شدهاند بصورت تصادفی به سه گروه تقسیم میشوند.
از گروه اول خواسته میشود برای یک مدت مشخص چای معمولی مصرف کنند، گروه دوم چای سبز و از گروه سوم خواسته میشود چای مصرف نکنند.
پس از پایان زمان آزمایش، میزان کاهش وزن شرکتکنندگان در هر سه گروه محاسبه و ثبت میشود.
سؤال پژوهشی اصلی این پژوهشگر این بوده است که آیا مصرف چای باعث کاهش وزن میشود یا نه. این سؤال باید به زبان آمار ترجمه شود:
زبان آمار: آیا تفاوت معنی داری بین میانگین سه گروه وجود دارد؟
اگر تفاوت بین میانگینهای این سه گروه به لحاظ آماری معنی دار نباشد، نتیجه گرفته میشود که مصرف چای تأثیری بر کاهش وزن نداشتهاست و در غیراین صورت، مصرف چای را در کاهش وزن مؤثر میدانیم.
مثال ۲٫
مدیر یک کارخانه تولید کیک و کلوچه تصمیم دارد ازبین ۴ بیکینگ پودر موجود در بازار یکی را انتخاب ودر خط تولیدخود مورداستفاده قراردهد.
در فرمول تولید کیک این کارخانه فقط یک عامل را متغیر درنظرمیگیرند و آن نوع بیکینگ پودر است.
پس بیکینگ پودر در این آزمایش، متغیر مستقل محسوب میگردد.
فرض کنید متغیر وابسته در این پژوهش حجم کیک تولیدشده باشد.
سؤال پژوهش در این تحقیق این است که کدام بیکینگ پودر برای خریداری بهتر است. به زبان آمار این سؤال پژوهشی بصورت زیر درمیآید:
آیا تفاوت معنی داری بین میانگین حجم کیکهای تولیدی در کارخانه وجود دارد یا نه؟
مثال ۳٫
مدیری میخواهد بهرهوری در شرکت خود را ازطریق افزایش سرعت کارکنان خود ازطریق استفاده از یک برنامه کامپیوتری خاص افزایش دهد.
وی معتقد است این مهارتها بین کارکنان وجود ندارد.
از این رو از یک مؤسسه آموزشی میخواهد تا آموزشهای مناسب را برای این برنامه کامپیوتری برای کارکنان تهیه کند.
این مؤسسه آموزشی ۳ دوره آموزشی را برای آموزش به کارکنان این شرکت به مدیر مربوطه ارائه کردهاند:
یک دوره مبتدی، یک دوره متوسط و یک دوره پیشرفته.
اما این مدیر در انتخاب دوره مناسب برای کارمندان دچار تردید شدهاست و مطمئن نیست که کدام دوره برای کارکنان مناسبتر است.
با توجه به این تردید، وی ۱۰ کارمند را در دوره ابتدایی، ۱۰ نفر را در دوره متوسط و ۱۰ نفر را در دوره پیشرفته ثبتنام میکند.
مدیر مربوطه بعد از آن که کارمندان از دوره آموزشی بازگشتند میخواهد بررسی کند که آیا تفاوتی بین مهارت کارکنان شرکتکننده در این دورههای آموزشی بوجودآمدهاست یا نه.
این مدیران برای آن که میزان مهارت را اندازهگیری کنند یک مسئله طراحیکرده و به کارکنان میدهد.
آیا میانگین زمان حل مسئله بین کارکنان متفاوت است؟

تحلیل واریانس (ANOVA)
تاریخچه تحلیل واریانس
مدلهای تحلیل واریانس (ANOVA) توسط سر رونال ای. فیشر (۱۸۹۰-۱۹۶۲) توسعه داده شد.
فیشر ابتدا واژه واریانس را معرفی کرد و آنالیز آن را ابتدا در مقالهای در سال ۱۹۱۸ منتشر نمود.
اما، اولین کاربرد تکنیک تحلیل واریانس در سال ۱۹۲۱ بوسیله فیشر ارائه گردید.
بعداز چاپ کتاب روشهای آماری برای محققین(Statistical Method for research workers)بوسیله فیشر،این روش بطورگستردهای شناختهشد.
چه شد که تحلیل واریانس بوجود آمد؟
فرض کنید که قرار است میانگین دو گروه از آزمودنی ها را باهم مقایسه کنیم. در این حالت، از آزمون t- مستقل (درحالت پارامتری) ویا U-من ویتنی (در حالت ناپارامتری) استفاده میکنیم.
مسئله وقتی پیش می آید که قرار باشد بیش از دو گروه داشته باشیم و بخواهیم تفاوتهای بین این گروهها را بررسی کنیم، در این حالت با ترکیبهای مختلفی از میانگینها مواجه خواهیم بود.
تحلیل واریانس (ANOVA)
مثلاً فرض کنید میخواهیم میانگین ۵ گروه را با هم مقایسه کنیم.
اگر بخواهیم از آزمون t-مستقل استفاده کنیم باید ۱۰ مقایسه انجام دهیم (یک مسئله ترکیبیات، انتخاب ۲ تا از ۵ تا).
مشکل انجام این مقایسات چند گروهی به مفهوم زمینهای تحلیل آماری بر میگردد.
هر آزمون بر اساس احتمال درست بودن فرضیه صفر است.
بنابراین، هر بار که آزمون را انجام میدهیم، خطر خطای نوع اول وجود دارد.
سطح احتمال در نقطهای تنظیم میشود که ما در آن فرضیه صفر را رد میکنیم و درعینحال سطحی است که ما خطر را در آن پذیرفتهایم.
اگر این سطح مثلا ۰٫۰۵ باشد، یعنی ما خطر ۵ بار از ۱۰۰ پذیرش فرضیه صفر غلط را پذیرفتهایم.
درهرصورت زمانی که آزمونهای t متعدد را با نمونههای مستقل که روی یک متغیر اندازهگیری میشود، انجام میدهیم. میزان خطا با تعداد آزمونهای انجامشده به صورت نمایی افزایش مییابد.
برای مثال در مسئله ۵ گروهی، میزان خطا ۰٫۲۲۶ خواهد بود.
برای جلوگیری از افزایش احتمال ایجاد خطای نوع اول،به جای بکارگیری یک سری مقایسات ازطریق t-مستقل، آزمون تحلیل واریانس طراحی و مطرح گردید.
تحلیل واریانس دارای پیشفرضهایی است که در صورت برقرارنبودن آنها باید از آزمون کروسکال والیس استفاده کرد.
در این مقاله پیشفرضهای تحلیل واریانس را بخوانید.
تحلیل واریانس (ANOVA)
فرض صفر و فرض مقابل در تحلیل واریانس
فرض صفر: میانگین گروهها با هم برابر هستند.
فرض مقابل: حداقل دو تا از میانگینها با هم برابر نیستند.
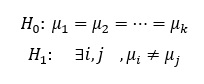
در رابطه اول همان چیزی به زبان ریاضی بیان شده که قبلا گفتم؛ یعنی، برابری میانگین ها.
در رابطه دوم، خلاف فرض صفر مطرح شدهاست. یعنی حداقل دو تا میانگین از بین میانگینها پیدا شوند که با هم برابر نباشند.
اگر فرض صفر در آزمون تحلیل واریانس پذیرفته شود به معنای آن است که تفاوت معنی داری بین سطوح مختلف متغیر مستقل وجود نداشته است.
به عبارت کاربردیتر میتوان گفت مداخله پژوهشگر مؤثر نبوده است.
تحلیل واریانس- قسمت دوم
ممکن است مطالب زیر نیز برای شما جذاب باشند:
مجذور اتا
آلفای کرونباخ
منابع آزمون دکتری- یک قطب نما
تا کنکور با شما هستیم… برای اطلاع از آخرین اخبار و مشاهده فیلمهای آموزشی دکتری و کارشناسی ارشد به صفحه اینستاگرام دیجی درس مراجعه نمایید:
صفحه اینستاگرام دیجی درس، دانشگاهی در خانه
خرید و دانلود محصولات کمک آموزشی کنکور کارشناسی ارشد و دکتری:
آمار
بسته جمعبندی آمار کارشناسی ارشد
پاسخ تشریحی آمار و روش تحقیق کارشناسی ارشد
بسته جمعبندی آمار کنکور دکتری
پاسخ تشریحی آمار و روش تحقیق دکتری


