
روش تحقیق تک آزمودنی
خرداد 8, 1398
طرح اشتغالزایی پویش دکتری
تیر 11, 1398حد و پیوستگی ، ریاضی ۱
یکی از دروس پایه و بسیار مهم برای دانشجویان کارشناسی بهویژه در رشتههای فنی و مهندسی درس ریاضی ۱ است.
از مهمترین سرفصلهای درس ریاضی ۱ میتوان به مباحثی چون حد و پیوستگی ، مشتق و انتگرال اشاره کرد.
در این صفحه به مرور مفاهیم اولیه حد و پیوستگی میپردازیم.
برای مشاهده فیلمهای آموزشی به صفحه اینستاگرام دیجی درس مراجعه نمایید:
صفحه اینستاگرام دیجی درس، دانشگاهی در خانه
ریاضی ۱
درس ریاضی عمومی ۱ زیربنای بسیاری از دروس در دوره کارشناسی است که دارای مفاهیم متنوع و درعینحال آشنا است.
این ویژگی موجب میشود تا امکان طرح سؤالات گوناگون برای اساتید فراهم آید.
از این رو دانشجویانی که تسلط کافی بر مباحث درس ریاضی ۱ نداشته باشند در روز امتحان با مشکل رویهرو خواهند شد.
برای موفقیت در امتحانات ریاضی عمومی ۱ به برنامهریزی برای مطالعه و حل سؤالات مختلف نیاز است.
سرفصلهای درس ریاضی عمومی ۱
ریاضی عمومی ۱ برای رشتههای فنی و مهندسی در دوره کارشناسی ۳ واحدی و برای رشتههای علوم پایه ۴ واحدی است.
مباحث عمده درس ریاضی ۱ که در تمامی رشتههای فنی و مهندسی، علوم پایه، مدیریت و حسابداری مشترک است عبارتند از:
– توابع
– حد و پیوستگی
– مشتق
– انتگرال
– دنباله و سری

حد و پیوستگی ، ریاضی عمومی ۱
نحوه مطالعه ریاضی ۱
ماهیت درس ریاضی ۱ بهگونهای است که صرفاً با خواندن نمیتوان برآن تسلط یافت.
یادگیری این درس به تمرین و حل مسائل متنوع نیاز دارد.
بنابراین دانشجویان باید نحوه استفاده از فرمولها و روشهای حل مسائل را به خوبی یاد بگیرند.
برای مطالعه گام به گام درس ریاضی ۱ و تسلط بر آن میتوانید اقدامات زیر را انجام دهید:
– یادگیری مفاهیم و فرمولها به طور دقیق
– مطالعه منابع ریاضی ۱ (جزوه و کتاب)
(مهمترین منابع برای درس ریاضی ۱ کتابهای توماس و لیتهلد میباشند.)
– حل مثالها و تمرینهای کتاب
نکته
تعداد مسائلی که حل میکنید نباید به قدری زیاد باشدکه از مباحث دیگر عقب بیفتید.
همانطورکه گفته شد درس ریاضی ۱ دارای مفاهیم متعددی است که تسلط بر همه آن ها کمی زمانبر است.
ازطرفی برخی از مفاهیم پیشنیاز مفاهیم دیگرند و تسلط بر آنها برای یادگیری دیگر مطالب الزامی است.
بنابراین باید به گونهای برنامهریزی نمایید که قبل از امتحان تمامی مطالب ریاضی ۱ را مطالعه کرده و بر آنها تسلط کافی داشته باشید.
حد و پیوستگی
حد و پیوستگی از مفاهیم بسیارمهم در درس ریاضی عمومی ۱ هستند.
آشنایی با این مفاهیم پیشنیاز یادگیری مفاهیم مر بوط به مشتق و کاربرد آن است.
در ادامه مروری مختصر بر مفاهیم اولیه حد و پیوستگی خواهیم داشت.
حد
یونانیهای عصر باستان نخستین افرادی بودهاند که درکی از مفهوم حد داشتهاند .
ارشمیدس با استفاده از مساحت چندضلعیهای منتظم محاط در دایره با شعاع یک درحالیکه تعداد اضلاع بدون کران افزایش مییابد مقدار تقریبی را محاسبه کرد.
در قرون وسطی و تا دوره رنسانس نیز از مفهوم حد برای محاسبه مساحت شکلهای گوناگون استفاده میشد.
حد یک مفهوم اساسی و کاربردی در ریاضی ۱ و مقدمه ای برای مفاهیم پیوستگی، مشتق و انتگرال است.
تعریف حد
در حالت کلی حد به معنی بررسی رفتار یک تابع اطراف یک نقطه خاص است.
اگر مقدار متغیر x در تابع f به یک عدد دلخواه مثل a بسیار نزدیک شود مقدار y در این تابع نیز به عددی مانند L نزدیک خواهد شد.
در این صورت L را حد تابع f در نقطه x=a مینامیم.
برای اینکه f در نقطه a دارای حد باشدکافی است همسایگی عدد a در دامنه تابع باشد و نیازی به وجود خود نقطه a در دامنه تابع نیست.
چنانچه متغیر x به مقدار a نزدیک شود ولی به آن نرسد میگوییم x به سمت a میل میکند.
در تعریف حد برای تابع f اگر x به a میل کند مقدار حاصل برابر با حد تابع یا L خواهد بود.
حد یک تابع به صورت زیر نمایش داده میشود:
تعریف حد
حد چپ تابع
فرض کنیم تابع f در بازه (a,x0) تعریف شده باشد.
چنانچه متغیر x این تابع ( با مقادیر کوچکتر از x0) به x0 میل کند مقدار تابع f به عدد L نزدیک خواهد شد.
در این صورت L را حد چپ تابع f مینامند و به صورت زیر نمایش میدهند:
حد چپ تابع
حد راست تابع
تابع f در بازه (x0,b) تعریف شدهاست.
چنانچه متغیر x این تابع ( با مقادیر بزرگتر از x0) به x0 میل کند مقدار تابع f به عدد L نزدیک خواهد شد.
در این صورت L را حد راست تابع f نامیده و به صورت زیر نمایش میدهند:
حد راست تابع
نتیجه:
اگر تابع f در بازههای (x0 ,b) و (a,x0) تعریف شدهباشد آنگاه حد تابع f در نقطه x0 برابر L است اگر و فقط اگر حد راست وحد چپ تابع در نقطه x0 موجود و مساوی L باشند.
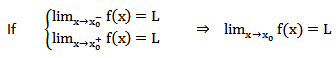
حد
قضایایی در مورد حد:
۱- حد تابع ثابت f(x)=c در هر نقطه مانند x0 برابر با مقدار ثابت c است.
۲- حد تابع f(x)=x در هر نقطه مانند x0 برابر با x0 است.
۳- حد تابع f(x)=ax+ b در هر نقطه مانند x0 برابر است با : ax0 + b.
۴- حد مجموع، تفاضل، حاصلضرب و خارج قسمت دو تابع
دو تابع f و g داریم که هردوی آنها در نقطه x0 دارای حد میباشند.
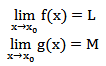
حد
در این صورت حد مجموع دو تابع برابر با مجموعه حد هریک از آنها است.
حد مجموع دو تابع
حد تفاضل دو تابع نیز برابر با تفاضل حد هر یک از آنها میباشد.
حد تفاضل دو تابع
حد حاصلضرب این دو تابع برابر با حاصلضرب حد هر یک از آنها است.
حد حاصلضرب دو تابع
حد حاصل تقسیم دو تابع برهم برابر با حاصل تقسیم حد هر یک از آنهاست به گونهای که مخرج صفر نشود.
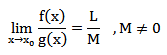
حد خارج قسمت دو تابع
نکته:
در محاسبه حد حاصل تقسیم دو تابع برهم چنانچه حد هردو تابع صفر باشد نمیتوان از قضیه حد خارج قسمت استفاده کرد.
در این صورت عبارت موردنظر مبهم است و باید ازطریق سادهسازی کسر ابهام را برطرف نمود.
پس از رفع ابهام میتوان حد کسر ساده شده را در نقطه x0 محاسبه کرد.
۵- حد تابع مرکب
اگر تابع g در x0 دارای حدی برابر با m باشد و حد تابع f نیز در (g(x0 موجود و برابر با M باشد آنگاه تابع fog در نقطه x0 دارای حدی برابر با M خواهد بود.
این قضیه بهویژه وقتی برقرار است که در همسایگی از x0 داشته باشیم: ![]()
تمام ویژگیهای فوق برای حد راست و حد چپ نیز صادق است.
قضیه فشردگی
چنانچه مقدار تابع (f(x وقتی x به x0 میل کند بین دو تابع (g(x و (h(x قرار داشته باشد و هردوی این توابع در ![]() دارای حدی برابر با L باشند، آنگاه حد تابع f نیز برابر با L خواهد بود.
دارای حدی برابر با L باشند، آنگاه حد تابع f نیز برابر با L خواهد بود.
حد نامتناهی
چنانچه مقادیر متغیر x را برای تابع f به مقدار کافی به x0 نزدیک کنیم و در پیآن مقدار تابع f به طور بیکران افزایش یابد و از هر عدد مثبتی بزرگتر شود داریم:
حد نامتناهی
دراینجا از علامت ![]() برای نمایش مقدار تابع در
برای نمایش مقدار تابع در ![]() استفاده میشود .
استفاده میشود .
در واقع ![]() یک عدد حقیقی نیست و بنابراین تایع در این حالت حد ندارد.
یک عدد حقیقی نیست و بنابراین تایع در این حالت حد ندارد.
به طور مشابه اگر مقادیر x در تابع f به x0 میل کنند و مقدار تابع به طور بیکران کاهش یابد و از هر عدد منفی کوچکتر شود داریم:
حد نامتناهی
در این حالت نیز حد تابع موجود نیست.
قضیه:
اگر دو تابع f و g به صورت زیر داشته باشیم:
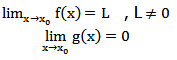
آنگاه:
– اگر L و (g(x هر دو در اطراف x0 مثبت باشند، داریم:
![]()
– اگر L مثبت و (g(x در اطراف x0 منفی باشد، داریم:
![]()
– اگر L منفی و (g(x در اطراف x0 مثبت باشد، داریم:
![]()
– اگر L منفی و (g(x در اطراف x0 منفی باشد، داریم:
![]()
این قضایا برای حدهای یک طرفه (حد راست و حد چپ) نیز صادق هستند.
جمع، تفاضل، حاصلضرب و خارج قسمت حدهای بی نهایت
اگر دو تابع f و g به صورت زیر داشته باشیم:
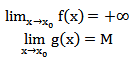
آنگاه:
برای M مثبت:
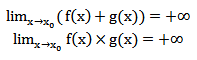
برای M منفی:
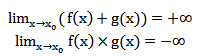
حدود فوق به طور مشابه برای حدهای ![]() نیز با توجه به علامت M برقرار هستند.
نیز با توجه به علامت M برقرار هستند.
مجانب قائم
اگر مقدار تابع f هنگامیکه به بی نهایت میل کند، آنگاه خط x=a را مجانب قائم نمودار تابع f میگوییم.
برای اینکه x=a مجانب قائم نمودار تابع f باشد باید حداقل یکی از حالتهای زیر رخ دهد:
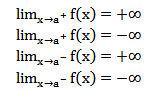
مجانب قائم
مجانب افقی
اگر و حد تابع f برابر با b شود، آنگاه خط y=b را مجانب افقی نمودار تابع f مینامیم.
مجانب افقی
معمولاً خطوط مجانب افقی یا مجانب قائم را با خط چین رسم میکنند.
قضایایی درمورد حد نامتناهی
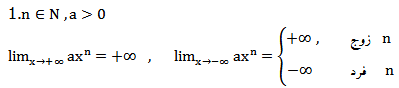
۲- اگر حد دو تابع (f(x و (g(x در ![]() نامتناهی و برابر با
نامتناهی و برابر با ![]() باشند آنگاه داریم:
باشند آنگاه داریم:
طبق قضیه فوق نمیتوان حد دو عبارت ![]() یا
یا ![]() را مشخص نمود.
را مشخص نمود.
برای یافتن حد این دو عبارت ابتدا باید رفع ابهام نمود و توابعی معادل با ![]() یا
یا ![]() بدست آورد و سپس حد این توابع معادل را تعیین کرد.
بدست آورد و سپس حد این توابع معادل را تعیین کرد.
یکی دیگر از حالتهای ابهام حالتی است که حد تابع (f(x برابر با ![]() یا
یا ![]() باشد و حد تابع (g(x برابر با صفر باشد.
باشد و حد تابع (g(x برابر با صفر باشد.
در این صورت حد تابع ![]() مشخص نیست.
مشخص نیست.
برای رفع ابهام در این حالت باید (f(x)g(x را به عبارتی مانند (h(x تبدیل نمود که حد آن در زمانی که ![]() برابر با حد عبارت فوق باشد.
برابر با حد عبارت فوق باشد.
پیوستگی
تابع f را در نقطه x0 از دامنهاش پیوسته گوییم هرگاه حد تابع در ![]() موجود و برابر با (f(x0 باشد.
موجود و برابر با (f(x0 باشد.
اگر یک تابع در تمام نقاط دامنه خود پیوسته باشد آن را تابعی پیوسته گوییم.
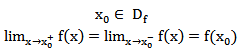
شرط پیوستگی
اگر ![]() میگوییم تابع در نقطه x0 دارای پیوستگی راست است.
میگوییم تابع در نقطه x0 دارای پیوستگی راست است.
چنانچه ![]() میگوییم تابع در نقطه x0 پیوستگی چپ دارد.
میگوییم تابع در نقطه x0 پیوستگی چپ دارد.
برای بررسی پیوستگی یک تابع ابتدا دامنه تابع را در نقطه مورد نظر بررسی کرده سپس مقدار تابع و حد چپ و حد راست تابع را محاسبه میکنیم.
نکته:
یک تابع چند جملهای در تمام نقاط حقیقی همواره پیوسته است.
قضیه:
اگر دو تابع f و g در x=x0 پیوسته باشند آنگاه قدرمطلق هریک از آنها و نیز توابع f+g ، f-g ، f.g در این نقطه پیوستهاند.
همچنین تابع f/g درصورتیکه دارای مخرج صفر نباشد و نقطه x0 در دامنه آن باشد پیوسته است.
پیوستگی ترکیب دو تابع
اگر تابع g در x0 پیوسته باشد و تابع f نیز در(g(x0 پیوسته باشد آنگاه تابع fog در نقطه x0 پیوسته خواهد بود.
پیوستگی در یک بازه
تابع f را در بازه باز (a,b) پیوسته مینامیم هرگاه f در تمام نقاط این بازه پیوسته باشد.
تابع f را در بازه باز [a,b] پیوسته مینامیم هرگاه f در تمام نقاط بازه (a,b) پیوسته باشد و حد تابع f در نقطه برابر (f(a و در نقطه برابر(f(b باشد.
نکاتی در مورد مبحث حد و پیوستگی
– اولین نکتهای که در حد باید به آن توجه کنید دامنه تابع است.
باید کنترل کنید که آیا تابع موردنظر میتواند به نقطه مربوطه میل کند یا نه.
– انواع ابهام و روشهای رفع آن را در محاسبه حد درنظرداشتهباشید.
– به تفاوت صفر مطلق و صفر حدی و قوانین مربوط به آنها توجه داشته باشید.
– تعریف حد در بی نهایت را به طور دقیق یاد بگیرید.
– روشهای اثبات وجود یا عدم وجود حد توسط دنبالهها را بیاموزید.
– پیش از حل سؤالات حد و پیوستگی به مبهم بودن یا نبودن عبارت موردنظر توجه کنید.
– دو مفهوم پیوستگی راست و پیوستگی چپ از نکات مهمی است که در حل سؤالات باید به آن توجه کنید.
برای دریافت مطالب فوق در یک فایل PDF اینجا کلیک کنید.
حد و پیوستگی ، ریاضی ۱
ممکن است مقالات زیر نیز برای شما جذاب باشند:


